본문 바로가기
AI 컴퓨터 비전프로젝트

[ML/DL] 파이토치로 구현한 논리회귀

by 바다의 공간 2024. 7. 23.

1. 단항 논리회귀(Logistic Regression)

  • 분류를 할 때 사용하며, 선형 회귀 공식으로부터 나왔기 때문에 논리회귀라는 이름이 붙여짐
  • 회귀 분석을 기반을 하지만 분류 문제에 사용
  • 주로 시그모이드 함수를 사용
    • 예측값을 0에서 1사이의 값으로 되도록 만듦
    • 0에서 1 사이의 연속된 값을 출력으로 하기 때문에 보통 0.5(임계값)을 기준으로 구분을 많이 합니다.
    • S자 곡선을 그리므로 미분 가능한 형태를 가지고 있어서 최적화가 용이합니다.
    • 주어진 입력값이 특정 클래스에 속할 확률을 계싼. 이진 분류 문제를 해결

  • 논리회귀는 입력 데이터 x에 대한 선형 결합 계산 -> 그 결과를 시그모이드 함수에 통과 시켜서 출력갑을 0과 1 사이의 값으로 변환 -> 이 값을 특정 클래스에 속할 확률로 해석
import torch
import torch.nn as nn

학습이 되었다는 전제하에~~

x = torch.tensor([1.0, 2.0, 3.0])
w = torch.tensor([0.1, 0.2, 0.3])
b = torch.tensor(0.5)

선형 결합계산을 해보면 아래와 같습니다.

# z= W1*x1 + W2*x2 + W3*x3 + b
# z = 0.1*1.0 + 0.2+2.0 + 0.3*3.0 + 0.5
z = torch.dot(w, x)+b
z
#tensor(1.9000)

이걸가지고 분류를 할 수 없으니 시그모이드를 사용합니다.

sigmoid = nn.Sigmoid()
output = sigmoid(z)
output
#tensor(0.8699)

기준을 0.5를 뒀다면 1로 나오게 되겠죠?

import torch.optim as optim
import matplotlib.pyplot as plt
torch.manual_seed(2024)

값이 변경되지않도록 시드값 고정 2024로 고정

 

데이터만들기

예를들어서 x는 공부한 시간이라고 가정하고 y중 0은 불합격 1은 합격이라고 가정합니다.

x_train = torch.FloatTensor([[0], [1], [3], [5], [8], [11], [15], [20]])
y_train = torch.FloatTensor([[0], [0], [0], [0], [1], [1], [1], [1]])
print(x_train.shape)
print(y_train.shape)

#torch.Size([8, 1])
#torch.Size([8, 1])
plt.figure(figsize=(8,5))
plt.scatter(x_train, y_train)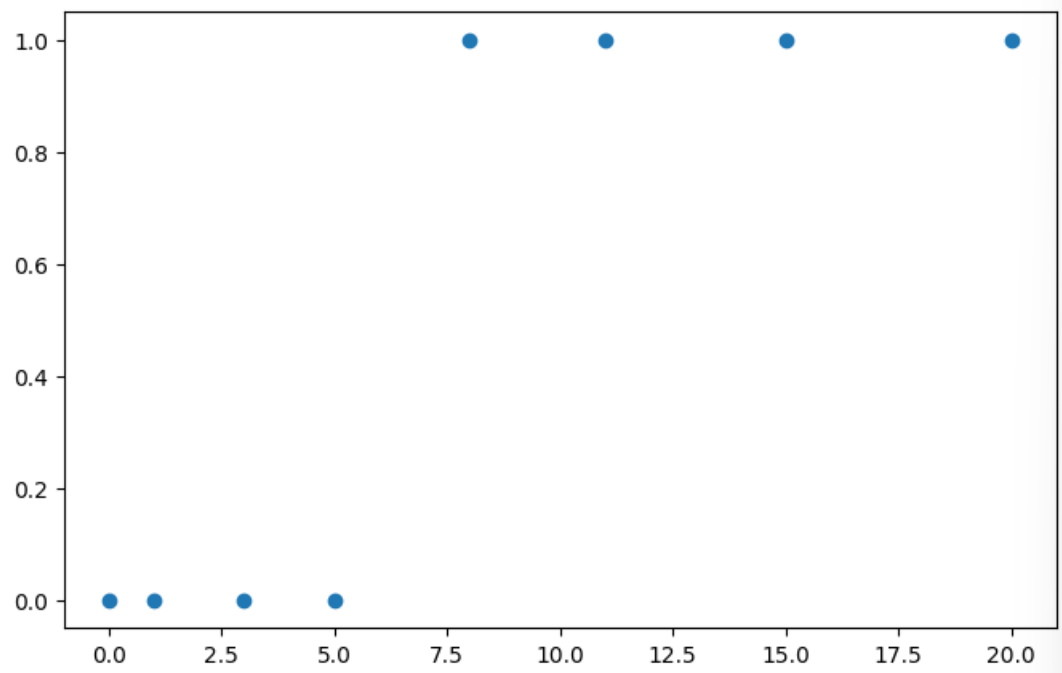

 

model = nn.Sequential(
    nn.Linear(1, 1),
    nn.Sigmoid()
)

model

#Sequential(
#  (0): Linear(in_features=1, out_features=1, bias=True)
#  (1): Sigmoid()
#)

(1) 은 시그모이드 함수를 돌려서 나간다 라고 생각하면 됩니다.

 

모델만든거 파라미터 확인해보기

list(model.parameters()) #W:[0.0634], b:[0.6625]

2. 비용함수

  • Binary Cross Entropy
  • 논리회귀에서는 nn.BCELoss() 함수를 사용해서 Loss를 계산합니다.
  • 1번시그마, 2번 시그마중에서 1번 시그마는 정답이 참이었을때 부분, 2번 시그마는 정답이 거짓이었을 때 부분
  • 정답이 1 - y값

앞쪽은 참인경우 오른쪽은 거짓인경우로 생각할 수 있습니다.

y_pred = model(x_train)
y_pred

#tensor([[0.6598],
#        [0.6739],
#        [0.7012],
#        [0.7270],
#        [0.7631],
#        [0.7958],
#        [0.8340],
#       [0.8734]], grad_fn=<SigmoidBackward0>)
loss = nn.BCELoss()(y_pred, y_train)
loss

#tensor(0.6901, grad_fn=<BinaryCrossEntropyBackward0>)

 

이 값을 줄여가야합니다.

optimizer = optim.SGD(model.parameters(), lr=0.01)
epochs = 1000

for epoch in range(epochs + 1):
    y_pred = model(x_train)
    loss = nn.BCELoss()(y_pred, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0:
        print(f'Epoch: {epoch}/{epochs} Loss: {loss:.6f}')

 

이렇게 학습을 시킨 후 파라미터를 확인해보면

list(model.parameters())

#[Parameter containing:
# tensor([[0.2875]], requires_grad=True),
# Parameter containing:
# tensor([-1.2444], requires_grad=True)]

회귀선을 그은것을 확인할 수 있습니다.

x_test = torch.FloatTensor([[10]])
y_pred = model(x_test)
y_pred

#tensor([[0.8363]], grad_fn=<SigmoidBackward0>)

시그모이드를 지났기에 확률로 나온것입니다.

그래서 임계치를 설정해주고 값을 확인해야하니까

임계치 설정해줍니다.

# 임계치 설정하기
# 0.5보다 크거나 같으면 1
# 0.5보다 작으면 0
y_bool = (y_pred >= 0.5).float()
y_bool

#tensor([[1.]])
#시험에 붙은것을 확인할 수 있다

 

여기까지 정리 다시해보자면~

단항 논리회귀는 둘 중 하나를 선택하는 분류문제를 사용할때 쓰는 방법이고
1. 선형 회기식을 먼저 사용
2. 시그모이드 함수에 넣어서 0과1 을 구별하도록 만들어줌

비용함수도 함께 공부했었다.
임계치를 설정하고 0.5보다 크거나 같으면 1 
0.5보다 작으면 0으로 설정했습니다.

 

3. 다항 논리회귀

데이터를 만들어보며 설정해봅니다.


x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 4, 5, 9],
           [1, 7, 7, 7],
           [2, 8, 7, 8]]

y_train = [0, 0, 0, 1, 1, 1, 2, 2]

 

클래스가 3개고 변수는 4개가 되어있습니다.

x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
print(x_train.shape)
print(y_train.shape)

#torch.Size([8, 4])
#torch.Size([8])




모델을 만들어봅니다.

model = nn.Sequential(
    nn.Linear(4, 3)
)
model

#Sequential(
#  (0): Linear(in_features=4, out_features=3, bias=True)
#)

지금은 리니어로 예측선을 넣어줄것입니다. 4개의변수가 있으니 4개의 기울기가 들어갑니다. 그리고 출력은 3개가 되겠죠

클래스가 3개니까요! (0,1,2의 클래스)

 

모델에 x_train을 넣어주고 y_pred로 예측해봅니다. (학습이 안 된 상황)

y_pred = model(x_train)
y_pred

#학습이 안 된 기울기에서 3개를 내뿜어달라고하니 아래의 값이 나옴
#tensor([[-0.3467,  0.0954, -0.5403],
#        [-0.3109, -0.0908, -1.3992],
#        [-0.1401,  0.1226, -1.3379],
#        [-0.4850,  0.0565, -2.1343],
#        [-4.1847,  1.6323, -0.7154],
#        [-3.6448,  2.2688, -0.0846],
#        [-5.1520,  2.1004, -0.9593],
#        [-5.2114,  2.1848, -1.0401]], grad_fn=<AddmmBackward0>)

그러면 이제오차를 계산하는 함수를 알아야하겠죠?

 

3-1.CrossEntropyLoss(교차엔트로피손실함수)

  • 교차 엔트로피 손실 함수 Pytorch에서 제공하는 손실 함수 중 하나로 다중클래스 분류 문제에서 사용하는 함수입니다.
  • 소프트맥스 함수와 교차 엔트로피 손실 함수를 결합한 형태입니다.
  • 소프트맥스 함수를 적용하여 각 클래스에 대한 확률 분포를 얻음
  • 각 클래스에 대한 로그 확률을 계산
  • 실제 라벨과 예측 확률의 로그 값 간의 차이를 계산
  • 계산된 차이의 평균을 계산하여 최종 손실 값을 얻음

3-2. SoftMax

  • 다중 클래스 분류 문제에서 사용되는 함수로 주어진 입력 벡터의 값을 확률 분포로 변환
  • 각 클래스에 속할 확률을 계산할 수 있으며, 각 요소를 0과 1사이의 값으로 변환해주고 이 값들의 합은 항상 1이 되도록 하는 형태를 가지고 있습니다.
  • 각 입력 값에 대해서 지수함수를 적용함
  • 지수함수를 적용한 모든 값의 합을 계산한 후, 각 지수의 합으로 나누어 정규화를 해줍니다.
  • 정규화를 통해 각 값은 0과 1사이의 확률값으로 출력됩니다.

로그 구하는 방법을 확인하기

3개 이상의 값을 구하는 함수

loss = nn.CrossEntropyLoss()(y_pred, y_train)
loss

#tensor(1.2760, grad_fn=<NllLossBackward0>)

1.2760만큼 틀렸다만큼 나오게 됩니다 굉장히 로스값이 크다는것을 알 수 있습니다.

 

#학습하기

optimizer = optim.SGD(model.parameters(), lr=0.01)

 

#에폭 돌려주기

epochs = 10000

for epoch in range(epochs + 1):
    y_pred = model(x_train)
    loss = nn.CrossEntropyLoss()(y_pred, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(f'Epoch: {epoch}/{epochs} Loss: {loss:.6f}')

 

#테스트값을 만들어주기.

x_test = torch.FloatTensor([[1, 9, 9, 8]])
y_pred = model(x_test)
y_pred

#tensor([[-25.1349,   4.4347,  15.2480]], grad_fn=<AddmmBackward0>)

이러면 2가 나와야되는것이죠(직접만든 그냥 test값)

 

#소프트맥스 사용하기

# nn.Softmax(1) == nn.Softmax(dim=1)
# 소프트맥스 함수를 적용할 차원을 지정
# dim=0일 경우 첫 번째 차원을 따라 소프트 맥스를 계산
# dim=1일 경우 두 번쨰 차원을 따라 소프트 맥스를 계산
# ...
# y_pred = torch.tensor([[1.0, 2.0, 3.0], [1.0, 2.0, 3.0])
y_prob = nn.Softmax(1)(y_pred)
y_prob

 

결과값이 e로 처리되기에 너무 깊게나오니까 다시 보기 쉽게 적어줍니다.

.2f를 이용하여 소수 둘째자리까지 표현해주도록 하겠습니다.

'''
세로로 보면
[1.0, 2.0, 3.0]
[1.0, 2.0, 3.0]

이렇게 결과값이나오게 됩니다.
열로볼 수 있지만 아니라는점을 알고있어야합니다.
'''
print(f'0일 확률: {y_prob[0][0]:.2f}')
print(f'1일 확률: {y_prob[0][1]:.2f}')
print(f'2일 확률: {y_prob[0][2]:.2f}')

#0일 확률: 0.00
#1일 확률: 0.00
#2일 확률: 1.00

 

 

 

이렇게 해도 좋지만 

한 번에 가장 높은 값을 뽑는 방법은 아규맥스를 사용해서 하면 됩니다.

torch.argmax(y_prob, axis=1)
#tensor([2])

로 2로 잘 예상하는것을 확인할 수 있습니다.

4. 경사 하강법의 종류

 

 

*종류가 두가지가있는데 실제로 2가지가있는것이아니라는점 주의

 

4-1. 배치 경사 하강법

  • 가장 기본적인 경사 하강법을 의미합니다(Vanilla Gradient Descent)
  • 데이터셋 전체를 고려하여 손실함수를 계산
  • 한 번의 Epoch에 모든 파마리터 업데이트를 단 한번만 수행하는것을 의미합니다.
  • 파라미터 업데이트할 때 한 번의 전체 데이터셋을 고려하기 떄문에 모델 학습시 많은 시간과 메모리가 필요하다는 단점이 있습니다.

4-2. 확률적 경사 하강법

  • 이것을 알고리즘화시킨것이 SGD알고리즘입니다.
  • 확률적 경사 하강법(Stochastic Gradient Descent)은 배치 경사 하강법이 모델 학습 시 많은 시간과 메모리가 필요하다는 단점을 보완하기 위해 제안된 기법입니다.
  • batch size를 1로 설정하여 파라미터를 업데이트 하기 때문에 배치 경사 하강법보다 훨씬 빠르고 적은 메모리로 학습을 진행
  • 파라미터 값의 업데이트 폭이 불안전하기 때문에 정확도가 낮은 경우가 생길 수 있음

4-3. 미니 배치 경사 하강법

  • 미니 배치 경사 하강법(Mini-Batch Gradient Descent)은 Batch Size를 설정한 size로 사용
  • 배치 경사 하강법보다 모델 속도가 빠르고, 확률적 경사 하강법보다 안정적인 장점이 있습니다.
  • 딥러닝 분야에서 가장 많이 활용되는 경사 하강법(테스트할때 사용하지 않음)
  • 일반적으로 Batch Size를 4, 8, 16, 32, 64, 128 과 같이 2의 n제곱에 해당하는 값으로 사용하는것이 관례적입니다.

5. 경사 하강법의 여러가지 알고리즘(torch)

 

5-1. SGD(확률적 경사 하강법)

  • 매개변수 값을 조정 시 전체 데이터가 아니라 랜덤으로 선택한 하나의 데이터에 대해서만 계산하는 방법(중복이 될 수 있음)

5-2. 모멘텀(Momentum)

  • 경사 하강법의 단점을 보완하기 위해 도입된 알고리즘 입니다.
  • 관성이라는 물리학 법칙을 응용한 방법입니다.
  • 접선의 기울기에 한 시점 이전의(바로 직전의) 접선의 기울기 값을 일정한 비율만큼 반영해서 그 다음거에 반영하는 방식으로 사용됩니다.
  • 이전 기울기의 이동 평균을 사용하여 현재 기울기를 업데이트한다고 생각하면 됩니다.
  • 반영하는 갯수를 정해주지만 보통은 90%를 설정해줍니다.
  • 가속도를 제공하기때문에 경사 하강법보다 빠르게 최소값에 도달할 수 있습니다.

5-3. 아다그라드(Adagrad)

  • 모든 매개변수에 동일한 학습률(lr)를 적용하는 것은 비효율적이다라는 생각에서 만들어진 학습 방법
  • 처음에는 크게 학습하다가 조금씩 작게 학습 시키는 형태입니다.
  • 각 파라미터에 맞춤형 학습률을 적용하는 방법
  • 희소한 데이터에 특히 유용하게 사용 (클래스가 되게 적은 경우에 유리함, 데이터 양 자체가 적은것이 아님을 주의하기)
  • 시간이 지남에 따라 학습률이 계속 감소하여 학습을 멈출 수 있습니다.

5-4. 아담(Adam)

  • Ad(아다그라드)와 am(모멘텀)를 합친 말이라고 생각하면 됩니다.
  • 기능이 서로 다르기에 둘 다 적용하면서 사용할 수 있습니다.
  • 최근에 가장 많이 사용합니다.
  • 각 매개변수에 대해 적응형 학습률을 적용하며 과거의 기울기 정보를 활용해 현재의 학습률을 조절할 수 있습니다.
  • AdamW : Adam의 변형으로 L2정규화(가중치 감쇠)를 별도로 처리하여 더 나은 일반화 성능을 제공, L2 정규화가 학습률 조정과 섞여서 불안정한 학습을 초래할 수 있는 문제를 해결했습니다.

6. 와인 품종 예측하기

  • sklearn.datasets.load_wine : 이탈리아의 같은 지역에서 재배된 세가지 다른 품종으로 만든 와인을 화학적으로 분석한 결과에 대한 데이터셋 (클래스가 3가지라는것을 알 수 있음)
  • 13개의 성분을 분석하여 어떤 와인인지 구별하는 모델을 구축
  • 데이터를 섞은 후, train 데이터를 80%를 잡고 test데이터를 20%로 하여 사용
  • Adam을 사용할것입니다.
    • 아담 사용방법 : optimizer = optim.Adam(model.parameters(), lr=0.01)
  • 테스트 데이터의 0번 인덱스가 어떤 와인인지 알아보고 정확도를 출력해보려고 합니다

#필요한 모듈 임포트

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

 

#데이터불러오기

이렇게 불러오면 x와 y데이터를 분할해서 받을 수 있습니다.

as_frame=True를 하게되면 애초부터 df로 받을 수 있습니다.(꿀팁)

x_data, y_data = load_wine(return_X_y=True, as_frame=True)

 

x데이터는 아래와 같습니다.

뒤에 더 있음

y데이터를 출력해보면

이렇게 나옵니다.

 

이제 텐서형으로 변경을 해줍니다

 

#텐서형으로 변경

x_data = torch.FloatTensor(x_data.values)
y_data = torch.LongTensor(y_data.values)

print(x_data.shape)
print(y_data.shape)

#torch.Size([178, 13])
#torch.Size([178])

x데이터는 벨류즈만 뽑아서 플로트 형으로 바꿔서 바꿔서 저장하고

y데이터는 longtensor형으로 변경해서 저장하는걸로 합니다.

 

#데이터 섞기 *8:2로 섞기 

x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.2, random_state=2024)

 

#데이터 모양 확인하기 

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

#torch.Size([142, 13]) torch.Size([142])
#torch.Size([36, 13]) torch.Size([36])

 

#모델 만들기

model = nn.Sequential(
    nn.Linear(13, 3)
)
optimizer = optim.Adam(model.parameters(), lr=0.01)

epochs = 1000

for epoch in range(epochs + 1):
    y_pred = model(x_train)
    loss = nn.CrossEntropyLoss()(y_pred, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0:
        y_prob = nn.Softmax(1)(y_pred)
        y_pred_index = torch.argmax(y_prob, axis=1)
        y_train_index = y_train
        accuracy = (y_pred_index == y_train_index).float().sum() / len(y_train) * 100
        print(f'Epoch {epoch:4d}/{epochs} Loss:{loss: .6f} Accuracy: {accuracy: .2f}%')

 

13개 받아서 3개 내보내줌( 3개의 클라스라서)

옵티마이저는 adam을 사용하게 되고 lr = 0.01을 주었습니다.

에포크는 1000으로 주고 CrossEntropyLoss를 이용하여 오차를 구하고

backward로 역전파시켜주고  zero_grad()로 초기화 시켜주고 

optimizer.step()으로 값을 넣어주게됩니다.

 

그리고 torch.argmax로 가장 확률이 높은값으로 가져오게 됩니다.

학습률이 98.59%로 아주 잘 된것같습니다.

 

#테스트값 넣어보기

y_pred = model(x_test)
y_pred[:5]

x_test값을 model에 넣어준 값을 y_pred에 넣어주고 그 값중 0,1,2,3,4까지 뽑아줍니다.

그 결과가 tensor로 5행으로 나오게 됩니다.

예측선에대한 값으로 나왔기 때문에 확률로 바꿔주게 됩니다.

 

#확률로 바꿔주기

y_prob = nn.Softmax(1)(y_pred)
y_prob[:5]

이 값들은 확률로 나오게 됩니다. 

 

#품종 출력해보기

print(f'0번 품종일 확률: {y_prob[0][0]:.2f}')
print(f'1번 품종일 확률: {y_prob[0][1]:.2f}')
print(f'2번 품종일 확률: {y_prob[0][2]:.2f}')

0번 품종일 확률: 0.00

1번 품종일 확률: 0.00

2번 품종일 확률: 1.00

으로 2번 품종일 확률이 100%라고 합니다.

 

코드해석 :  y_prob의 0의 0번, y_prob의 0의 1번, y_prob의 0의 2번    

저기서는 첫번째 와인이 0번일 확률 1번일 확률 2번일 확률을 구하는것입니다.

 

만약 2번의 와인을 구하려고 하면 

y_prob[2][0]:.2f

y_prob[2][1]:.2f

y_prob[2][2]:.2f

이렇게 구하면되겠죠!

 

 

#테스트 정확도 확인하기

y_pred_index = torch.argmax(y_prob, axis=1)
accuracy = (y_pred_index == y_test).float().sum() / len(y_test) * 100
print(f'테스트 정확도는: {accuracy:.2f}% 입니다!')

테스트 정확도는 94.44% 입니다! 로 출력되게 됩니다.

 

코드해석

1줄 :  제일 높은 확률의 데이터를 가져옵니다

2줄 : y_test와 y_pred_index가 같을경우에 folat로 합치고 나누고 *100하면 정확도를 갖게됩니다.

3줄 : 테스트 트레이닝 정확도를 예측할 수 있습니다.

 

torch.dot() 주로 벡터 간의 유사성을 측정하거나, 선형 대수학에서 두 벡터의 내적을 구할 때 사용됩니다.
nn.Sigmoid() 시그모이드 함수
nn.Sequential() 연산을 여러개 겹쳐서 넣을 수 있음.
 torch.FloatTensor
 로 연속적인 값(예: 실수)을 다루는 작업에 사용됩니다. 딥러닝 모델의 가중치, 편향 등 대부분의 연산에 사용됩니다.
torch.LongTensor
 주로 이산적인 값(예: 정수)을 다루는 작업에 사용됩니다. 예를 들어, 인덱스, 클래스 레이블 등을 표현할 때 사용됩니다.
BCELoss
 주로 이진 분류(Binary Classification) 문제에서 사용됩니다. 모델의 예측 값(확률)과 실제 라벨(0 또는 1) 간의 손실을 계산합니다.
nn.CrossEntropyLoss()(y_pred, y_train)
 주로 다중 클래스 분류(Multi-Class Classification) 문제에서 사용됩니다. 모델의 예측 로그 확률 분포와 실제 클래스 간의 손실을 계산합니다.
optimizer = optim.Adam(model.parameters(), lr=0.01) 아담 사용방법 : optimizer = optim.Adam(model.parameters(), lr=0.01)

 

저작자표시

'AI 컴퓨터 비전프로젝트' 카테고리의 다른 글

[DL] 균등화, 평탄화 등 이미지 변환 활용(이미지, 영상 품질관련)(1)  (0) 2024.09.27
[DL] YOLO의 흐름 확인하기 좋은 복습 글  (3) 2024.09.27
[ML] kMeans_비지도학습, 마케팅데이터셋 활용  (1) 2024.07.16
[ML]로지스틱 회귀_승진 될지 안 될지 분류해보기  (2) 2024.07.07
[ML] 선형 회귀_Rent값 예측 모델 만들기(2)  (0) 2024.07.04

관련글

티스토리툴바