Rent값 예측 모델 만들기
전체 과정
- 데이터 분할: 데이터를 훈련 데이터와 테스트 데이터로 나누기.
- 모델 학습: 훈련 데이터를 사용해 모델을 학습시키기.
- 모델 평가: 테스트 데이터를 사용해 모델이 얼마나 잘 예측하는지 평가하기.
- 예측: 학습된 모델을 사용해 새로운 데이터의 임대료를 예측하기.
으로 구성되어있고 이번 글은 2번~4번에 해당하는 글 입니다.
2. 선형 회귀(Linear Regression)기법
*리니어=Linear
- 데이터를 통해 데이터를 가장 잘 설명할 수 있는 직선으로 데이터를 분석하는 방법
- 단순 선형 회기분석(단일 독립변수를 이용)-사실 잘 사용하지 않음(독립변수가 하나인경우는 거의 없기에..)
- 다중 선형 회기분석(다중 독립변수를 이용)
from sklearn.linear_model import LinearRegression사이킷런 안에있는 리니어 모델안에있는 리니어 레그레션을 이용하려 합니다.
lr = LinearRegression()
lr.fit(X_train, y_train)객체를 만들고 fit(,학습) 시켜줄겁니다.
pred = lr.predict(X_test)
예측하기까까지 만들어줍니다.
3. 머신러닝 평가 지표 만들기
-머신러닝, 딥러닝은 숫자이기때문에 숫자가 낮아지게 만드는게 더 좋다.
- 예측값과 실제값의 차이에 대한 제곱에 대해 평균을 낸 값
- (1n)∑ni=1(yi−xi)2
- 마이너스가 생기게되면 안되기에 제곱을 해줌
예측값과 실제값 제공
p = np.array([3,4,5]) #예측값
act = np.array([1,2,3]) #실제값예측값과 실제값이 이미 틀려있습니다.
mse를 이용한 함수 만들기
def my_mse(pred, actual):
return((pred - actual) **2).mean()
결과값 확인하기
my_mse(p, act)
# 4.04.0으로 나왔지만 숫자가 작아져야하기때문에 더 낮아지게 만들어야합니다.
3-2. MAE(Mean Absolute Error)
- 예측값과 실제값의 차이에 대한 절대값에 대해 평균을 낸 값
- (1n)∑ni=1|yi−xi|
def my_mae(pred, actual):
return(pred - actual).mean()
my_mae(p, act)
#2.0
2가 나옵니다. 절대값을 씌었으니 제곱보다는 값이 적게 나옵니다.
3-3. RMSE(Root Mean Squared Error) (★)
- 예측값과 실제값의 차이에 대한 제곱에 대해 평균을 낸 후 루트를 씌운 값
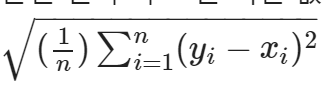
def my_rmse(pred, actual):
return np.sqrt(my_mse(pred, actual))
my_rmse(p, act)
#2.0
사이킷런에있는 모듈 사용하기
from sklearn.metrics import mean_absolute_error, mean_squared_error
MAE
mean_absolute_error(p, act)결과는 2.0이 나옵니다.
MSE
mean_squared_error(p, act)결과는 4.0이 나옵니다.
RMSE
mean_squared_error(p, act, squared=False)
결과는 2.0이 나옵니다.
학습이 끝난 상태에서 얼마만큼 오차가 나 있는지 데이터를 가지고 확인하도록 하겠습니다
3-4. 평가지표 적용하기
mean_squared_error(y_test, pred)
#1426204740.330996mean_absolute_error(y_test, pred)
#21997.237341647397mean_squared_error(y_test, pred, squared=False)
#37765.125980605386만큼의 오차가 발생했다고 합니다.
여기까지 예측선을 만들어놓은거라고 할 수 있습니다.
이상치에 대한 값을 뺀 후 학습 및 평가 해보기
-전처리를 조금 다르게 했을때의 차이를 알아보기
위에서 발견한 이상치인 1837을 drop해보려고 합니다.
만약 1837이 train에 있으면 잘 지워질거고 train에 없으면 에러가 나겠죠!
먼저 지워보겠습니다
X_train.drop(1837, inplace=True)
y_train.drop(1837, inplace=True)에러가 나지 않았습니다. 즉 데이터에는 1837이 있다는것을 확인할 수 있었습니다.
이제는 train쪽에서 값을 지웠으니 이상치에 대한 값이 없다는거겠죠?
이상치가 사라진 값으로 다시 객체를 새롭게 만들어보겠습니다.
lr2 = LinearRegression()새로 만든 이유는
전야학습때문에 그렇습니다. 기존에 있던 학습을 기반으로 해서 추가학습을 하게되면 성능이 좋아지니
전처리를 다르게 한 의미가 없으니까 새로 만들었습니다.
그 후 다시 fit(학습) 하겠습니다.
lr2.fit(X_train, y_train)
4. 예측하기
pred2 =lr2.predict(X_test)
mean_squared_error(y_test, pred2, squared=False)
#37731.275512059074
이제 위에서 이상치가 있는 값이 있는 학습과
이상치를 뺀 학습의 비교를 해보겠습니다.
| rmse | 이상치 유 | 이상치 무 | |
| 이름 | pred rmse | pred2 rmse | |
| 값 | 37765.125980605386 | 37731.275512059074 | |
| 오차 차이 | 33.850468546423286 | ||
33.85정도로 오차값이 줄어든 이상치 무 가 더 성능이 좋다는것을 알게 되었습니다.
이로써 데이터 전처리가 왜 중요한지 알 수 있었습니다
리뷰
| 공부할 | 설명 |
| lr.fit(X_train, y_train) | 넣고픈 x,y레이블값을 넣으면 학습이 끝남 |
'AI > 머신러닝' 카테고리의 다른 글
| [ML] kMeans_비지도학습, 마케팅데이터셋 활용 (1) | 2024.07.16 |
|---|---|
| [ML]로지스틱 회귀_승진 될지 안 될지 분류해보기 (2) | 2024.07.07 |
| [ML] 선형 회귀_Rent값 예측 모델 만들기(1) (0) | 2024.07.02 |
| [ML] 아이리스 데이터셋(Iris DataSet) (1) | 2024.07.01 |
| [Python] 판다스(pandas) 데이터 프레임 합치기,산술연산, 원핫인코딩 등 (1) | 2024.06.18 |



