🟢분산분석
🟢분산분석(ANOVA)
분산분석(ANOVA)은 여러 집단(3개 이상)의 평균 차이를 통계적으로 유의미한지 검정
- 일원 분산 분석 (One-way ANOVA): 하나의 요인(독립변수)에 따라 평균의 차이 검정
- 예를들어 식물의 성장(종속변수)이있을때 물의 양(독립변수) 에 따라 어떤 차이가 있는지?
- 이원 분산 분석 (Two-way ANOVA): 두 개의 요인 (독립변수) 에 따라 평균의 차이 검정
- 예를들어 식물의 성장(종속변수)이있을때 물의 양(독립변수), 햇빛(독립변수)에 따라 어떤 차이가 있는지?
🟢 일원 분산 분석
- 3개 이상의 집단 간의 평균의 차이가 통계적으로 유의한지 검정
- 하나인 요인이고, 집단의 수가 3개 이상일 때 사용
🟢기본가정
- 독립성: 각 집단의 관측치는 독립적이다.
- 정규성: 각 집단은 정규분포를 따른다. (샤피로 검정)
- 등분산성: 모든 집단은 동일한 분산을 가진다. (레빈 검정)
🟢 귀무가설과 대립가설
- 귀무가설: 모든 집단의 평균은 같다.
- 대립가설: 적어도 한 집단은 평균이 다르다. (집단의 평균의 차이가 있다)
🟢일원 분산 분석
# 사이파이
f_oneway(sample1, sample2, ...)F_onewayResult(statistic=7.2969837587007, pvalue=0.0006053225519892207)
# 스테츠모델즈 (아노바 테이블)
model = ols('종속변수 ~ 요인', data = df).fit()
print(anova_lm(model))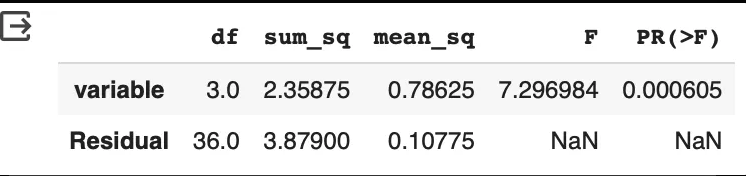
- df: 자유도
- sum_sq: 제곱합 (그룹 평균 간의 차이를 나타내는 제곱합)
- mean_sq: 평균 제곱 (sum_sq/자유도)
- F: 검정통계량
- PR(>F): p-value
아노바 테이블은 조금 더 많은 정보들을 가지고있습니다.
🟢 프로세스
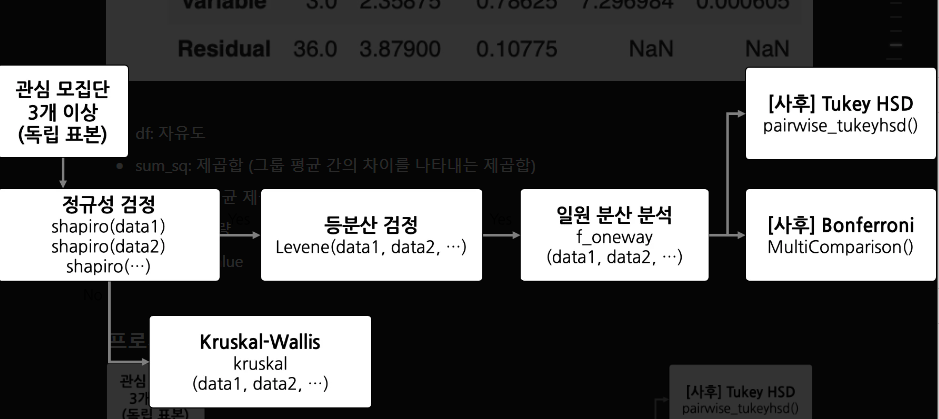
일원분산분석으로는 어떤 값의 차이가 있는지를 모르기때문에 사후검정을 통해서 어떤 그룹이 다른지를 확인할 수 있다.
🟢사후검정 방법
투키(tukey)
group1 group2 meandiff p-adj lower upper reject
A B 0.41 0.0397 0.0146 0.8054 True
A C 0.09 0.9273 -0.3054 0.4854 False
A D -0.27 0.2722 -0.6654 0.1254 False
B C -0.32 0.1483 -0.7154 0.0754 False
B D -0.68 0.0003 -1.0754 -0.2846 True
C D -0.36 0.0852 -0.7554 0.0354 Falsepadj는 pvalue라고 보면 됨.
reject이 true면 0.05보다 작은것!
본페로니(bonferroni)
group1 group2 stat pval pval_corr reject
A B -2.7199 0.014 0.0843 False
A C -0.515 0.6128 1.0 False
A D 1.7538 0.0965 0.5788 False
B C 2.2975 0.0338 0.2028 False
B D 6.0686 0.0 0.0001 True
C D 2.5219 0.0213 0.1279 Falsepval =기본 pvalue이고 보정된 pvalue는 pval-corr입니다.
reject이 true면 0.05보다 작은것!
🟢 이원 분산 분석
- 3개 이상의 집단 간의 평균의 차이가 통계적으로 유의한지 검정
- 요인의 수가 2개, 집단의 수가 3개 이상일 때 사용
🟢 기본가정
- 독립성: 각 집단의 관측치는 독립적이다.
- 정규성: 각 집단은 정규분포를 따른다. (샤피로 검정)
- 등분산성: 모든 집단은 동일한 분산을 가진다. (레빈 검정)
🟢 귀무가설과 대립가설
-각각 요인별로 귀무,대립을 넣어야함
주 효과와 상호작용 효과
- 주 효과(요인1)
- 귀무가설: 모든 그룹의 첫 번째 요인의 평균은 동일하다.
- 대립가설: 적어도 두 그룹은 첫 번째 요인의 평균은 다르다.
- 주 효과(요인2)
- 귀무가설: 모든 그룹의 두 번째 요인의 평균은 동일하다.
- 대립가설: 적어도 두 그룹은 두 번째 요인의 평균은 다르다.
- 상호작용효과
- 귀무가설: 두 요인의 그룹 간에 상호작용은 없다.
- 대립가설: 두 요인의 그룹 간에 상호작용이 있다.
🟢 이원 분산 분석
# 스테츠모델즈 (아노바 테이블)
model = ols('종속변수 ~ C(요인1) * C(요인2)', data=df).fit()
print(anova_lm(model))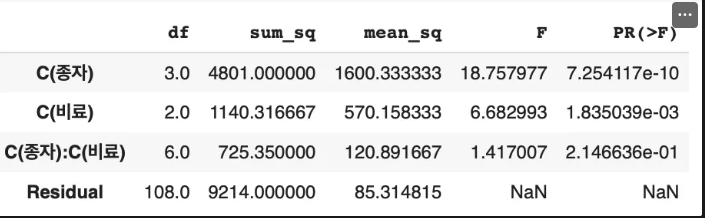

'자격증 > [빅분기] 빅데이터분석기사' 카테고리의 다른 글
| [작업형2] roc_acu_score 에러. (1) | 2024.11.18 |
|---|---|
| [작업형3] 일원분산분석 실습 + 심화실습 (0) | 2024.11.17 |
| [작업형3] 다선형회귀, 범주형이 섞여있다면? (0) | 2024.11.14 |
| [작업형3] 회귀분석-단순 선형 회귀 분석 (3) (0) | 2024.11.13 |
| [작업형3] 회귀분석- 상관관계 (2) (0) | 2024.11.12 |



